菜到怀疑人生

0%

剑指offer上

发表于 更新于 分类于
本文字数： 23k 阅读时长 ≈ 38 分钟

前言：剑指offer上

二维数组中的查找

解法1:二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * @author shency
 * @description: TODO
 */
public class Solution {
    public boolean Find(int target, int[][] array) {
        for (int i = 0; i < array.length; i++) {
            int left = 0;
            int right = array[i].length - 1;
            while (left <= right) {
                int mid = (left + right) / 2;
                if(array[i][mid] == target){
                    return true;
                }else if(array[i][mid]< target){
                    left = mid + 1;
                }else{
                    right = mid - 1;
                }
            }
        }
        return false;
    }
}

解法2:利用二维数组由上到下，由左到右递增的规律，那么选取右上角或者左下角的元素a[row][col]与target进行比较

当target小于元素a[row][col]时，那么target必定在元素a所在行的左边,即col–；

当target大于元素a[row][col]时，那么target必定在元素a所在列的下边,即row++；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @author shency
 * @description: TODO
 */
public class Solution {
    public boolean Find(int target, int[][] array) {
        if (array == null) {
            return false;
        }
        int width = array[0].length;
        int height = array.length;
        int row = 0, col = width - 1;
        // 从右上角开始
        while (row < height && col >= 0) {
            if (array[row][col] == target) {
                return true;
            } else if (array[row][col] < target) {
                row++;
            } else {
                col--;
            }
        }
        return false;
    }
}

替换空格

解法1:string的replaceAll函数

1
2
3
4
5
public class Solution {
    public String replaceSpace(StringBuffer str) {
       return str.toString().replaceAll("\\s", "%20");
    }
}

解法2:遍历string

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * @author shency
 * @description: TODO
 */
public class Solution {
    public String replaceSpace(StringBuffer str) {
        StringBuffer result = new StringBuffer();
        for (int i = 0; i < str.length(); i++) {
            if (str.charAt(i) == ' ') {
                result.append("%20");
            } else {
                result.append(str.charAt(i));
            }
        }
        return result.toString();
    }
}

从尾到头打印链表

链表节点

1
2
3
4
5
6
7
8
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}

解法1:遍历链表并储存在ArrayList中，然后反转ArrayList

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import java.util.ArrayList;
import java.util.Collections;
/**
 * @author shency
 * @description: TODO
 */
public class Solution {
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        ArrayList<Integer> list = new ArrayList<>();
        while (listNode != null){
            list.add(listNode.val);
            listNode =  listNode.next;
        }
        Collections.reverse(list);
        return list;
    }
}

解法2:递归

1
2
3
4
5
6
7
8
9
10
11
import java.util.ArrayList;
public class Solution {
    private ArrayList<Integer> list = new ArrayList<>();
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        if (listNode != null){
            printListFromTailToHead(listNode.next);
            list.add(listNode.val);
        }
        return list;
    }
}

重建二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import java.util.Arrays;

public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        if(pre.length == 0||in.length == 0){
            return null;
        }
        TreeNode node = new TreeNode(pre[0]);
        for(int i = 0; i < in.length; i++){
            if(pre[0] == in[i]){
                node.left = reConstructBinaryTree(Arrays.copyOfRange(pre, 1, i+1), Arrays.copyOfRange(in, 0, i));
                node.right = reConstructBinaryTree(Arrays.copyOfRange(pre, i+1, pre.length), Arrays.copyOfRange(in, i+1,in.length));
            }
        }
        return node;
    }
}

用两个栈实现队列

一个做出队列，一个做入队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();

    public void push(int node) {
        stack1.push(node);
    }

    public int pop() {
        if (stack1.empty() && stack2.empty()) {
            throw new RuntimeException("Queue is empty!");
        }
        if (stack2.empty()) {
            while (!stack1.empty()) {
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
}

旋转数字的最小数字

二分查找

需要考虑三种情况

(1)array[mid] > array[right]

出现这种情况的array类似[3,4,5,6,0,1,2]，此时最小数字一定在mid的右边。
left = mid + 1

(2)array[mid] == array[right]

出现这种情况的array类似 [1,0,1,1,1] 或者[1,1,1,0,1]，此时最小数字不好判断在mid左边
还是右边,这时只好一个一个试 ，
right = right - 1

(3)array[mid] < array[right]

出现这种情况的array类似[2,2,3,4,5,6,6],此时最小数字一定就是array[mid]或者在mid的左
边。因为右边必然都是递增的。
right = mid

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
    public int minNumberInRotateArray(int[] array) {
        if (array == null || array.length == 0) {
            return 0;
        }
        int left = 0, right = array.length - 1;
        while (left < right) {
            int mid = (left + right) / 2;
            if (array[mid] > array[right]) {
                left = mid + 1;
            } else if (array[mid] < array[right]) {
                right = mid;
            } else {
                right = right - 1;
            }
        }
        return array[left];
    }
}

斐波那契数列

斐波那契数列指的是这样一个数列 1, 1, 2, 3, 5, 8, 13, 21……

这个数列从第3项开始，每一项都等于前两项之和。

1
2
3
4
5
6
7
8
9
10
public class Solution {
    public int Fibonacci(int n) {
        int sum = 0, f = 1;
        for (int i = 0; i < n; i++) {
            sum += f;
            f = sum - f;
        }
        return sum;
    }
}

跳台阶

表面是跳台阶，实际是斐波那契数列

f(1) = 1, f(2) = 2, f(3) = 3, f(4) = 5， 可以总结出f(n) = f(n-1) + f(n-2)的规律，但是为什么会出现这样的规律呢？假设现在6个台阶，我们可以从第5跳一步到6，这样的话有多少种方案跳到5就有多少种方案跳到6，另外我们也可以从4跳两步跳到6，跳到4有多少种方案的话，就有多少种方案跳到6，其他的不能从3跳到6什么的啦，所以最后就是f(6) = f(5) + f(4)；

1
2
3
4
5
6
7
8
public int JumpFloor(int target) {
    int sum = 1, f = 1;
    for (int i = 0; i < target - 1; i++) {
        sum += f;
        f = sum - f;
    }
    return sum;
}

变态跳台阶

f(0) = 1
f(1) = 1
f(2) = f(1) + f(0) = 2f(1)
f(3) = f(2) + f(1) + f(0) = 2f(2)
f(4) = f(3) + f(2) + f(1) + f(0) = 2f(3)
f(n) = 2f(n-1)

1
2
3
4
5
6
7
8
9
10
public int JumpFloorII(int target) {
    if (target == 0 || target == 1) {
        return 1;
    }
    int num = 1;
    for (int i = 2; i <= target; i++) {
        num = num * 2;
    }
    return num;
}

矩形覆盖

找规律，斐波那契数列
0 1 2 3 5 8

1
2
3
4
5
6
7
8
9
10
11
public int RectCover(int target) {
    if (target == 0) {
        return 0;
    }
    int sum = 1, f = 1;
    for (int i = 0; i < target - 1; i++) {
        sum += f;
        f = sum - f;
    }
    return sum;
}

二进制中1的个数

1
2
3
4
5
6
7
8
9
10
11
12
public class Solution {
    public int NumberOf1(int n) {
        int count = 0;
        String s = Integer.toBinaryString(n);
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '1') {
                count++;
            }
        }
        return count;
    }
}

数值的整数次方

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public double Power(double base, int exponent) {
        if (base == 0) {
            return 0;
        }
        if (exponent == 0) {
            return 1;
        }
        double result = 1;
        for (int i = 0; i > exponent; i--) {
            result = result * (1 / base);
        }
        for (int i = 0; i < exponent; i++) {
            result = result * base;
        }
        return result;
    }
}

调整数组顺序使奇数位于偶数前面

新建集合存放偶数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public void reOrderArray(int[] array) {
        int len = array.length;
        int k = 0;
        List<Integer> list = new ArrayList<>();
        for (int i = 0; i < len; i++) {
            if (array[i] % 2 == 0) {
                list.add(array[i]);
            } else {
                array[k++] = array[i];
            }
        }
        for (int i = k; i < len; i++) {
            array[i] = list.get(i - k);
        }
    }
}

冒泡

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public void reOrderArray(int[] array) {
        for (int i = 0; i < array.length - 1; i++) {
            for (int j = 0; j < array.length - 1 - i; j++) {
                if (array[j] % 2 == 0 && array[j + 1] % 2 == 1) {
                    int t = array[j];
                    array[j] = array[j + 1];
                    array[j + 1] = t;
                }
            }
        }
    }
}

链表中倒数第k个结点

stack

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public ListNode FindKthToTail(ListNode head, int k) {
        LinkedList<ListNode> stack = new LinkedList<ListNode>();
        ListNode p = head;
        while (p != null) {
            stack.push(p);
            p = p.next;
        }
        if (k > stack.size() || k == 0) {
            return null;
        }
        return stack.get(k - 1);
    }
}

双指针:指针p和q，p先走K步，使两指针相差K，然后一起走，p为null时，q就是倒数第K个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public ListNode FindKthToTail(ListNode head, int k) {
        ListNode p = head, q = head;
        int count = k;
        while (count-- > 0) {
            if (p == null) {
                return null;
            }
            p = p.next;
        }
        while (p != null) {
            p = p.next;
            q = q.next;
        }
        return q;
    }
}

反转链表

三个指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public ListNode ReverseList(ListNode head) {
        ListNode p = head, pre = null, cur = null;
        while (p != null) {
            cur = p.next;
            p.next = pre;
            pre = p;
            p = cur;
        }
        return pre;
    }
}

合并两个排序的链表

队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public ListNode Merge(ListNode list1, ListNode list2) {
        if (list1 == null && list2 == null) {
            return null;
        }
        LinkedList<ListNode> queue = new LinkedList<ListNode>();
        while (list1 != null || list2 != null) {
            if (list1 == null) {
                queue.add(list2);
                list2 = list2.next;
            } else if (list2 == null) {
                queue.add(list1);
                list1 = list1.next;
            } else if (list1.val < list2.val) {
                queue.add(list1);
                list1 = list1.next;
            } else {
                queue.add(list2);
                list2 = list2.next;
            }
        }
        ListNode head = queue.remove(), p = head;
        while (!queue.isEmpty()) {
            p.next = queue.remove();
            p = p.next;
        }
        return head;
    }
}

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public ListNode Merge(ListNode list1, ListNode list2) {
        if (list1 == null) {
            return list2;
        } else if (list2 == null) {
            return list1;
        }
        ListNode p = null;
        if (list1.val < list2.val) {
            p = list1;
            p.next = Merge(list1.next, list2);
        } else {
            p = list2;
            p.next = Merge(list1, list2.next);
        }
        return p;
    }
}

树的子结构

树节点

1
2
3
4
5
6
7
8
9
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;
    }
}

递归:判断tree1和tree2是否相同，先判断根节点是否相同，相同则调用isTreeEqual判断子节点是否相同；如果根节点不同，则判断tree1子树与tree2是否相同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public boolean HasSubtree(TreeNode root1, TreeNode root2) {
        if (root1 == null || root2 == null) {
            return false;
        }
        boolean flag = false;
        if (root1.val == root2.val) {
            flag = isTreeEqual(root1, root2);
        }
        if (!flag) {
            flag = HasSubtree(root1.left, root2);
        }
        if (!flag) {
            flag = HasSubtree(root1.right, root2);
        }
        return flag;
    }

    private boolean isTreeEqual(TreeNode root1, TreeNode root2) {
        if (root2 == null) {
            return true;
        }
        if (root1 == null) {
            return false;
        }
        if (root1.val != root2.val) {
            return false;
        }
        return isTreeEqual(root1.left, root2.left) && isTreeEqual(root1.right, root2.right);
    }
}

二叉树的镜像

先序遍历，交换左右子节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {
    public class TreeNode {
        int val = 0;
        TreeNode left = null;
        TreeNode right = null;

        public TreeNode(int val) {
            this.val = val;

        }
    }

    public void Mirror(TreeNode root) {
        if (root == null) {
            return;
        }
        if (root.left == null && root.right == null) {
            return;
        }
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        Mirror(root.left);
        Mirror(root.right);
    }
}

顺时针打印矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class Solution {
    public ArrayList<Integer> printMatrix(int[][] matrix) {
        if (matrix == null) {
            return null;
        }
        // 行
        int row = matrix.length;
        // 列
        int column = matrix[0].length;
        ArrayList<Integer> list = new ArrayList<Integer>();
        // 圈数
        int circle = ((row < column ? row : column) + 1) / 2;
        for (int i = 0; i < circle; i++) {
            // 从左往右
            for (int j = i; j < column - i; j++) {
                list.add(matrix[i][j]);
            }
            // 从上到下
            for (int k = i + 1; k < row - i; k++) {
                list.add(matrix[k][column - i - 1]);
            }
            // 从右向左
            for (int m = column - i - 2; (m >= i) && (row - i - 1 != i); m--) {
                list.add(matrix[row - i - 1][m]);
            }

            // 从下往上
            for (int n = row - i - 2; (n > i) && (column - i - 1 != i); n--) {
                list.add(matrix[n][i]);
            }
        }
        return list;
    }
}

包含min函数的栈

如何保存最小元素？
添加一个成员变量用于保存最小元素，但是这样会有一个问题, 如果最小元素被弹出了呢, 如何获得下一个最小元素呢? 所以仅仅添加一个成员变量存放最小元素是不够的,

我们需要在最小元素弹出后还能得到次小元素, 次小的弹出后, 还要能得到次次小的.

因此, 用另一个栈来保存这些元素是再合适不过的了. 最小元素栈,每次压栈操作时,如果压栈元素比当前最小元素更小, 就把这个元素压入最小元素栈, 原本的最小元素就成了次小元素. 同理, 弹栈时, 如果弹出的元素和最小元素栈的栈顶元素相等, 就把最小元素的栈顶弹出.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    LinkedList<Integer> stack = new LinkedList<Integer>();
    LinkedList<Integer> minStack = new LinkedList<Integer>();

    public void push(int node) {
        if (minStack.isEmpty() || node <= minStack.peek()) {
            minStack.push(node);
        }
        stack.push(node);
    }

    public void pop() {
        int node = stack.pop();
        if(node == minStack.peek()){
            minStack.pop();
        }
    }

    public int top() {
        return stack.peek();
    }

    public int min() {
        return minStack.peek();
    }
}

栈的压入、弹出序列

使用辅助栈，pushA数组逐个进栈，如果栈顶等于出栈一个元素，就pop并将pop顺序向后移动一位，最后检测辅助栈是否为空

举例：

入栈1,2,3,4,5

出栈4,5,3,2,1

首先1入辅助栈，此时栈顶1≠4，继续入栈2

此时栈顶2≠4，继续入栈3

此时栈顶3≠4，继续入栈4

此时栈顶4＝4，出栈4，弹出序列向后一位，此时为5，,辅助栈里面是1,2,3

此时栈顶3≠5，继续入栈5

此时栈顶5=5，出栈5,弹出序列向后一位，此时为3，,辅助栈里面是1,2,3

依次执行，最后辅助栈为空。如果不为空说明弹出序列不是该栈的弹出顺序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    LinkedList<Integer> stack = new LinkedList<Integer>();

    public boolean IsPopOrder(int[] pushA, int[] popA) {
        int k = 0;
        for (int i : pushA) {
            stack.push(i);
            while(!stack.isEmpty() && popA[k] == stack.peek()){
                stack.pop();
                k++;
            }
        }
        return stack.isEmpty();
    }
}

从上往下打印二叉树

广度搜索，使用队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {

    public class TreeNode {
        int val = 0;
        TreeNode left = null;
        TreeNode right = null;

        public TreeNode(int val) {
            this.val = val;
        }
    }

    public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
        ArrayList<Integer> list = new ArrayList<>();
        LinkedList<TreeNode> queue = new LinkedList<>();
        if (root == null) {
            return list;
        }
        queue.add(root);
        while (!queue.isEmpty()) {
            TreeNode t = queue.remove();
            list.add(t.val);
            if (t.left != null) {
                queue.add(t.left);
            }
            if (t.right != null) {
                queue.add(t.right);
            }
        }
        return list;
    }
}

二叉搜索树的后序遍历序列

  • 二叉搜索树的特性是左子树上所有的结点均小于根结点、右子树所有的结点均大于根结点。
  • 后序遍历是左右根，序列的最后一个元素为二叉树的根节点

基于上述特点，算法如下

  1. 确定root；
  2. 遍历序列（除去root结点），找到第一个大于root的位置，则该位置左边为左子树，右边为右子树；
  3. 遍历右子树，若发现有小于root的值，则直接返回false；
  4. 分别判断左子树和右子树是否仍是二叉搜索树（即递归步骤1、2、3）。

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public boolean VerifySquenceOfBST(int[] sequence) {
        if (sequence == null || sequence.length == 0) {
            return false;
        }
        return judge(sequence, 0, sequence.length - 1);
    }

    private boolean judge(int[] arr, int l, int r) {
        if (l >= r) {
            return true;
        }
        int i = r;
        while (i > l && arr[i - 1] > arr[r]) {
            --i;
        }

        for (int j = i - 1; j >= l; --j) {
            if (arr[j] > arr[r]) {
                return false;
            }
        }
        return judge(arr, l, i - 1) && (judge(arr, i, r - 1));
    }
}

非递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * @author shency
 * @description: TODO
 * @date: 2019/10/24
 */
public class Solution {
    public boolean VerifySquenceOfBST(int[] sequence) {
        int size = sequence.length;
        if (0 == size){
            return false;
        }

        int i = 0;
        while (--size >= 0) {
            while (sequence[i] < sequence[size]) {
                i++;
            }
            while (sequence[i] > sequence[size]) {
                i++;
            }
            if (i < size) {
                return false;
            }
            i = 0;
        }
        return true;
    }
}

二叉树中和为某一值的路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {
    ArrayList<ArrayList><Integer>> pathList = new ArrayList<>();
    ArrayList<Integer> list = new ArrayList<Integer>();

    public ArrayList<ArrayList><Integer>> FindPath(TreeNode root, int target) {
        preorder(root, target);
        // 降序排序
        Collections.sort(pathList, (o1, o2) -> o2.size() - o1.size());
        return pathList;
    }

    private void preorder(TreeNode root, int target) {
        if (root == null) {
            return;
        }
        list.add(root.val);
        // root是叶子结点且root.val == target
        if (root.val == target && root.left == null && root.right == null) {
            pathList.add(new ArrayList<Integer>(list));
        }
        FindPath(root.left, target - root.val);
        FindPath(root.right, target - root.val);
        // 回溯
        list.remove(list.size() - 1);
    }
}

复杂链表的复制

第一步：复制每个结点，如复制结点A得到A1，将结点A1插到结点A后面；

image-20191224003055178

第二步：遍历链表，复制老结点的随机指针给新结点，如A.next.random = A.random.next;

image-20191224003112440

第三步：拆分链表，将链表拆分为原链表和复制后的链表
image-20191224003126284

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class Solution {
    public RandomListNode Clone(RandomListNode pHead) {
        if (pHead == null) {
            return null;
        }
        RandomListNode p = pHead;
        while (p != null) {
            RandomListNode t = new RandomListNode(p.label);
            t.next = p.next;
            p.next = t;
            p = t.next;
        }
        p = pHead;
        while (p != null) {
            p.next.random = p.random == null ? null : p.random.next;
            p = p.next.next;
        }
        
        p = pHead;
        RandomListNode head = pHead.next;
        while(p != null) {
            RandomListNode cloneNode = p.next;
            p.next = cloneNode.next;
            cloneNode.next = cloneNode.next==null?null:cloneNode.next.next;
            p = p.next;
        }
        return head;
    }
}

二叉搜索树与双向链表

二叉搜索树、有序，所以选择中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Solution {
    private TreeNode head = null;
    private TreeNode p = null;
    public TreeNode Convert(TreeNode pRootOfTree) {
        preorder(pRootOfTree);
        return head;
    }
    private void preorder(TreeNode root) {
        if (root == null) {
            return;
        }
        preorder(root.left);
        if(head==null){
            head = root;
            p = head;
        }else{
            p.right = root;
            root.left = p;
            p = root;
        }
        preorder(root.right);
    }
}

全排列

递归+回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * @author shency
 * @description: TODO
 * @date: 2019/11/26
 */
public class Solution {
    private ArrayList<String> list = new ArrayList<>();

    public ArrayList<String> Permutation(String str) {
        if (str != null && str.length() > 0) {
            PermutationHelper(str.toCharArray(), 0);
            Collections.sort(list);
        }
        return list;
    }

    private void PermutationHelper(char[] cs, int i) {
        if (i == cs.length - 1) {
            String val = String.valueOf(cs);
            // 原字符串有相同字符，经全排列就会有重复字符串，如aa的全排列有aa、aa两种，需要去重。当然也可以选择不交换来避免
            if (!list.contains(val)) {
                list.add(val);
            }
        } else {
            for (int j = i; j < cs.length; j++) {
                swap(cs, i, j);
                PermutationHelper(cs, i + 1);
                swap(cs, i, j);
            }
        }
    }

    private void swap(char[] cs, int i, int j) {
        char temp = cs[i];
        cs[i] = cs[j];
        cs[j] = temp;
    }
}

数组中出现次数超过一半的数字

如果有符合题目条件的数字，则它出现的次数肯定比其他所有数字出现的次数和还要多。

保存第一个数字，遍历数组，若与保存的数字相同，则次数加1，否则次数减1；若次数为0，则保存下一个数字，并将次数置为1。遍历结束后，再判断它是否符合条件。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class Solution {
    public int MoreThanHalfNum_Solution(int[] array) {
        if (array == null || array.length == 0) {
            return 0;
        }
        int len = array.length;
        int num = array[0];
        int count = 1;
        for (int i = 1; i < len; i++) {
            if (array[i] == array[i - 1]) {
                count++;
            } else {
                count--;
                if (count == 0) {
                    num = array[i];
                    count = 1;
                }
            }
        }
        count = 0;
        for (int i : array) {
            if (num == i) {
                count++;
            }
        }
        return count > len / 2 ? num : 0;
    }
}

最小的K个数

ArrayList + Collections.sort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * @author shency
 * @description: TODO
 * @date: 2019/11/26
 */
public class Solution {
    public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) {
        ArrayList<Integer> list = new ArrayList<>();
        // 注意当k > input.length时需要返回空list
        if (k <= 0 || k > input.length) {
            return list;
        }
        for (int i : input) {
            list.add(i);
        }
        Collections.sort(list);
        return new ArrayList<Integer>(list.subList(0, k));
    }
}

PriorityQueue(最小堆)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Solution {
    public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) {
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        ArrayList<Integer> list = new ArrayList<>();
        if (k <= 0 || k > input.length) {
            return list;
        }
        for (int i : input) {
            queue.add(i);
        }
        while (k-- > 0) {
            list.add(queue.poll());
        }
        return list;
    }
}

连续子数组的最大和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Solution {
    public int FindGreatestSumOfSubArray(int[] array) {
        if (array == null || array.length == 0) {
            return 0;
        }
        int len = array.length;
        int sum = array[0];
        int max = array[0];
        for (int i = 1; i < len; i++) {
            sum = sum + array[i];
            if (sum > max) {
                max = sum;
            }
            if (sum <= 0) {
                sum = 0;
            }
        }
        return max;
    }
}

整数中1出现的次数（从1到n整数中1出现的次数）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class Solution {
    public int NumberOf1Between1AndN_Solution(int n) {
        if (n <= 0) {
            return 0;
        }
        long count = 0;
        for (long i = 1; i <= n; i *= 10) {
            long diviver = i * 10;
            long highNumber = n / (10 * i);
            long currentNumber = (n / i) % 10;
            long lowNumber = n - (n / i) * i;
            // 如果为0,出现1的次数由高位决定,count等于高位数字 * 当前位数
            if (currentNumber == 0) {
                count += highNumber * i;

            }
            // 如果为1,出现1的次数由高位和低位决定,count等于高位*当前位+低位+1
            else if (currentNumber == 1) {
                count += highNumber * i + lowNumber + 1;
            }

            //如果大于1,出现1的次数由高位决定,count等于（高位数字+1）* 当前位数
            else {
                count += (highNumber + 1) * i;
            }
        }
        return (int)count;
    }
}

把数组排成最小的数

  1. 将int数组转化为String数组
  2. String数组排序，规则自定义
  3. String数组拼接为String
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class Solution {
    public String PrintMinNumber(int[] numbers) {
        if (numbers == null || numbers.length == 0) {
            return "";
        }
        int len = numbers.length;
        String[] strings = new String[numbers.length];
        for (int i = 0; i < len; i++) {
            strings[i] = String.valueOf(numbers[i]);
        }
        Arrays.sort(strings, new Comparator<String>() {
            @Override
            public int compare(String o1, String o2) {
                String s1 = o1 + o2;
                String s2 = o2 + o1;
                return s1.compareTo(s2);
            }
        });
        StringBuilder stringBuilder = new StringBuilder();
        for (String s : strings) {
            stringBuilder.append(s);
        }
        return stringBuilder.toString();
    }
}

丑数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class Solution {
    public int GetUglyNumber_Solution(int index) {
        if (index <= 6) {
            return index;
        }
        int m2 = 0, m3 = 0, m5 = 0;
        ArrayList<Integer> list = new ArrayList<>();
        list.add(1);
        while (list.size() < index) {
            int n2 = list.get(m2) * 2;
            int n3 = list.get(m3) * 3;
            int n5 = list.get(m5) * 5;
            int num = Math.min(n2, Math.min(n3, n5));
            list.add(num);
            if (num == n2) {
                m2++;
            }
            if (num == n3) {
                m3++;
            }
            if (num == n5) {
                m5++;
            }
        }
        return list.get(list.size() - 1);
    }
}

第一个只出现一次的字符

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {
    public int FirstNotRepeatingChar(String str) {
        int len = str.length();
        int[] letter = new int[58];
        for (int i = 0; i < len; i++) {
            letter[str.charAt(i) - 'A']++;
        }
        for (int i = 0; i < len; i++) {
            if (letter[str.charAt(i) - 'A'] == 1) {
                return i;
            }
        }
        return -1;
    }
}

逆序对

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public class Solution {
    public int InversePairs(int[] array) {
        if (array == null || array.length == 0) {
            return 0;
        }
        int[] copy = array.clone();
        int count = mergeSort(array, copy, 0, array.length - 1);
        return count;

    }

    private int mergeSort(int[] array, int[] copy, int low, int high) {
        if (low == high) {
            return 0;
        }
        int mid = (low + high) >> 1;
        int leftCount = mergeSort(array, copy, low, mid);
        int rightCount = mergeSort(array, copy, mid + 1, high);
        int count = 0;
        int i = mid;
        int j = high;
        int locCopy = high;
        while (i >= low && j > mid) {
            if (array[i] > array[j]) {
                count += j - mid;
                copy[locCopy--] = array[i--];
                if (count >= 1000000007) {
                    count %= 1000000007;
                }
            } else {
                copy[locCopy--] = array[j--];
            }
        }
        while (i >= low) {
            copy[locCopy--] = array[i--];
        }
        while (j > mid) {
            copy[locCopy--] = array[j--];
        }
        System.arraycopy(copy, low, array, low, high - low + 1);
        return (leftCount + rightCount + count) % 1000000007;
    }
}

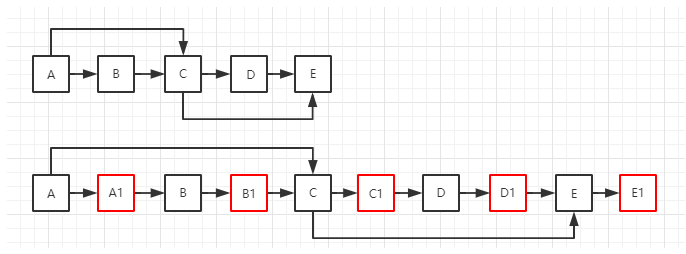
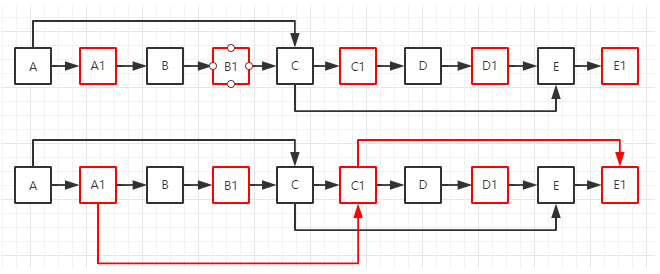
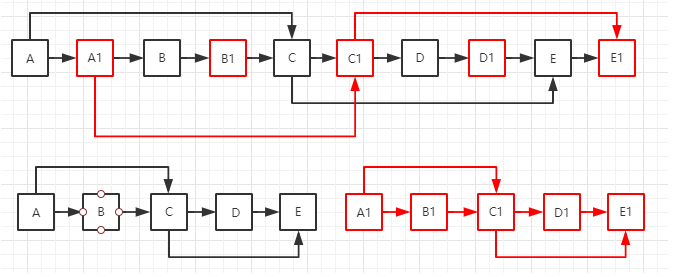
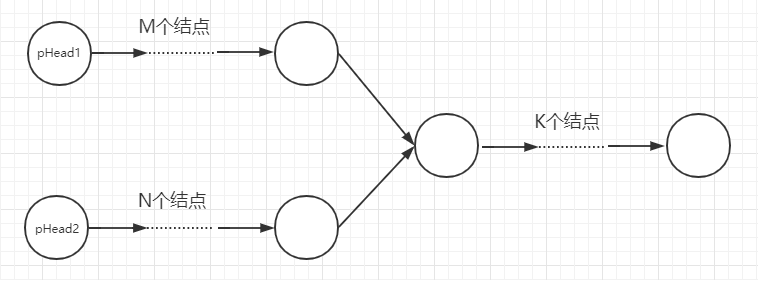
两个链表的第一个公共结点

image-20191224003016181

1
2
3
4
5
6
7
8
9
10
11
public class Solution {
    public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        ListNode p1 = pHead1;
        ListNode p2 = pHead2;
        while (p1 != p2) {
            p1 = (p1 == null ? pHead2 : p1.next);
            p2 = (p2 == null ? pHead1 : p2.next);
        }
        return p1;
    }
}

长度相同有公共结点，第一次就遍历到；没有公共结点，走到尾部NULL相遇，返回NULL

长度不同有公共结点，第一遍差值就出来了，第二遍必然一起到公共结点；没有公共，一起到结尾NULL。

也可以使用Set或Map的特性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
    public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        HashMap<ListNode, Integer> map = new HashMap<ListNode, Integer>();

        ListNode p1 = pHead1;
        ListNode p2 = pHead2;
        while (p1 != null) {
            map.put(p1, p1.val);
            p1 = p1.next;
        }
        while (p2 != null) {
            if (map.containsKey(p2)) {
                return p2;
            }
            p2 = p2.next;
        }
        return null;
    }
}
-------------本文结束感谢您的阅读-------------