堆排序

前言：总结堆排序

堆

堆是一种非线性结构，是一个完全二叉树，但本文是堆的数组实现

大顶堆

每个结点的值都大于或等于其左右孩子结点的值

arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

升序—-使用大顶堆

小顶堆

每个结点的值都小于或等于其左右孩子结点的值

arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

降序—-使用小顶堆

堆排序的思想

将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值，如此反复执行，便能得到一个有序序列了

实例 堆排序过程

自己画的图，有点丑……

堆的初始化

int a[6] = {7, 3, 8, 5, 1, 2};

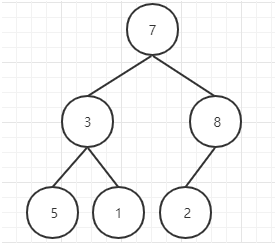
先要找到最后一个非叶子节点，数组的长度为6，那么最后一个非叶子节点就是：长度/2-1，也就是6/2-1=2，然后下一步就是比较该节点值和它的子树值，如果该节点小于其左、右子树的值就交换（意思就是将最大的值放到该节点）

8只有一个左子树，左子树的值为2，8>2不需要调整

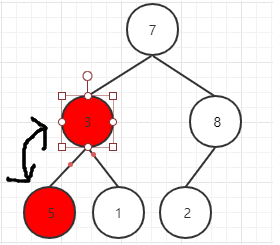
下一步，继续找到下一个非叶子节点（其实就是当前坐标-1就行了），该节点的值为3小于其左子树的值，交换值，交换后该节点值为5，大于其右子树的值，不需要交换

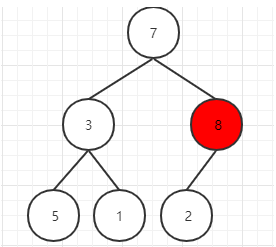
下一步，继续找到下一个非叶子节点，该节点的值为7，大于其左子树的值，不需要交换，再看右子树，该节点的值小于右子树的值，需要交换值

下一步，检查调整后的子树，是否满足大顶堆性质，如果不满足则继续调整（这里因为只将右子树的值与根节点互换，只需要检查右子树是否满足，而8>2刚好满足大顶堆的性质，就不需要调整了，如果运气不好整个数的根节点的值是1，那么就还需要调整右子树）

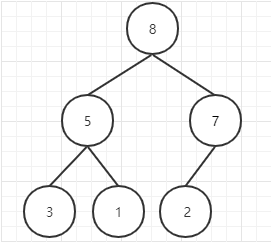
到这里大顶堆的构建就算完成了

开始堆的调整（下沉）

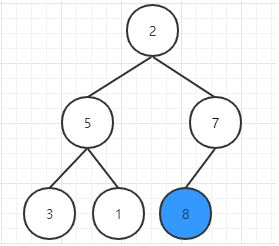
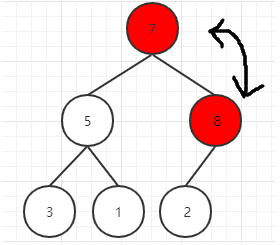
交换根节点（8）与最后一个元素（2）交换位置（将最大元素”沉”到数组末端），此时最大的元素就归位了

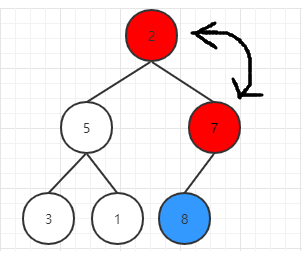
由于已经实现了堆的初始化，因此此时堆的最大值就是根节点的左右节点之一，也就是图中的5和7，因此我们直接将根节点与左右节点最大值交换

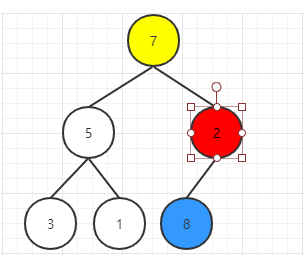
此时，我们已经确保根节点就是目前的最大值了，但是需要将2下沉，使堆重新满足每个结点的值都大于或等于其左右孩子结点的值。当然由于已经没有叶子节点，所以下沉结束。

堆顶与堆尾交换

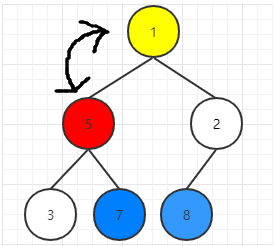
根节点1与左右节点最大值即5交换，此时5就是堆的最大值，将1下沉，即与左右子节点比较并交换

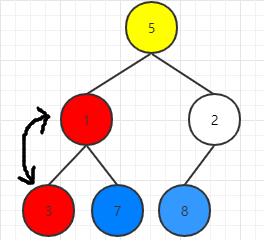
没有叶子节点，下沉结束

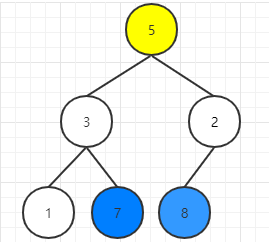
堆顶与堆尾交换

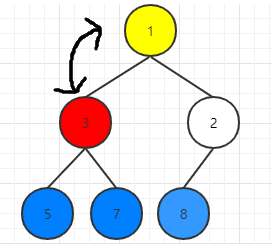
根节点1与左右节点最大值即5交换，此时5就是堆的最大值，将1下沉，即与左右子节点比较并交换

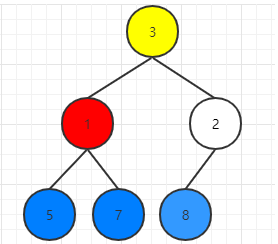
此时，3就是堆的最大值，1没有叶子节点，下沉结束

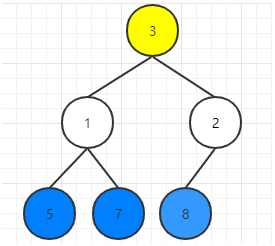
堆顶与堆尾交换

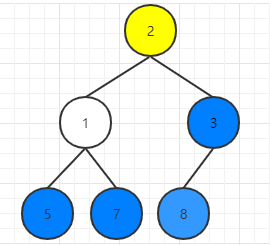
2节点比叶子节点都大，所以下沉结束，直接堆顶与堆尾交换

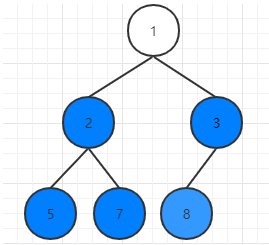
堆大小为1，运行结束

代码实现

PS：这里使用数组实现堆排序而不是树

public class Solution {
    public static void main(String[] args) {
        int[] nums = {16, 7, 74, 34, 45, 34, 55, 66, 3, 20, 17, 8};
        headSort(nums);
        for (int num : nums) {
            System.out.print(num + " ");
        }
    }

    /**
     * 堆排序
     */
    private static void headSort(int[] list) {
        //构造初始堆,从第一个非叶子节点开始调整,左右孩子节点中较大的交换到父节点中
        for (int i = (list.length) / 2 - 1; i >= 0; i--) {
            maxHeapAdjust(list, list.length, i);
        }
        //排序，将最大的节点放在堆尾，然后从根节点重新调整
        for (int i = list.length - 1; i >= 1; i--) {
            int temp = list[0];
            list[0] = list[i];
            list[i] = temp;
            maxHeapAdjust(list, i, 0);
        }
    }

    /**
     * 每一次堆调整，会使堆中每个结点的值都大于或等于其左右孩子结点的值，list[0]根节点成为最大值
     */
    private static void maxHeapAdjust(int[] list, int len, int i) {
        int k = i, temp = list[i], index = 2 * k + 1;
        while (index < len) {
            if (index + 1 < len) {
                if (list[index] < list[index + 1]) {
                    index = index + 1;
                }
            }
            if (list[index] > temp) {
                list[k] = list[index];
                k = index;
                index = 2 * k + 1;
            } else {
                break;
            }
        }
        list[k] = temp;
    }
}